KMP
1.1 前言
kmp,是一种用于字符串匹配的线性算法,复杂度 ,其中 为文本串, 为模式串。
名字来源:Knuth(D.E.Knuth) & Morris(J.H.Morris) & Pratt(V.R.Pratt)
1.2 引入
我们知道,朴素的字符串匹配是 的。
我们使用两个指针 和 ,并逐位比对。( 为文本串, 为模式串)
For(i,1,la)
{
bool flg=1;
For(j,1,lb)
{
if(a[i+j-1] != b[j])
{
flg=0;
break;
}
}
if(flg)
cout<<i<<endl;
}
那么,怎么优化呢?
1.3 优化
我们知道,对于 指针,最好的情况就是单调不减;但是对于 ,我们可以想办法让他在「失配」后尽可能少往前移动。
概念:
定义一个字符串 的 为 的一个非 本身的子串 ,满足 既是 的前缀,又是 的后缀。
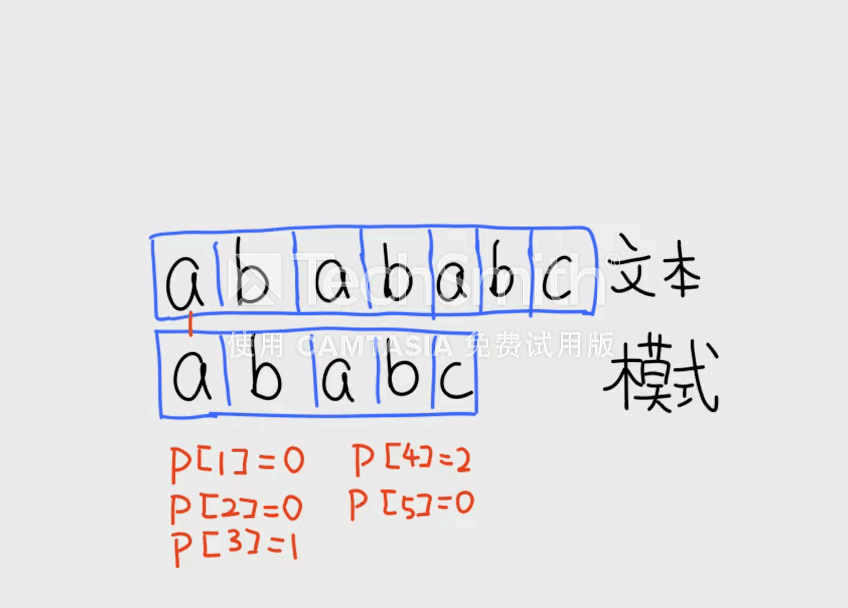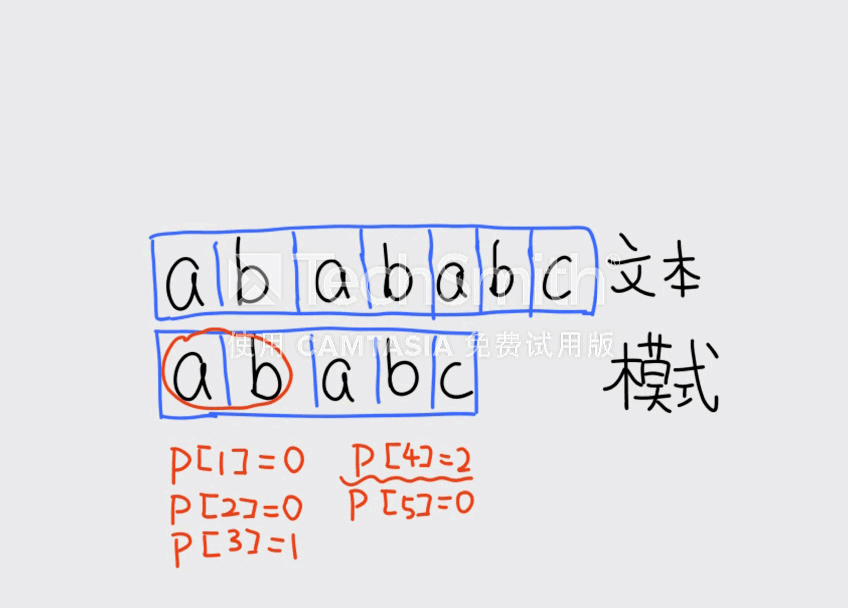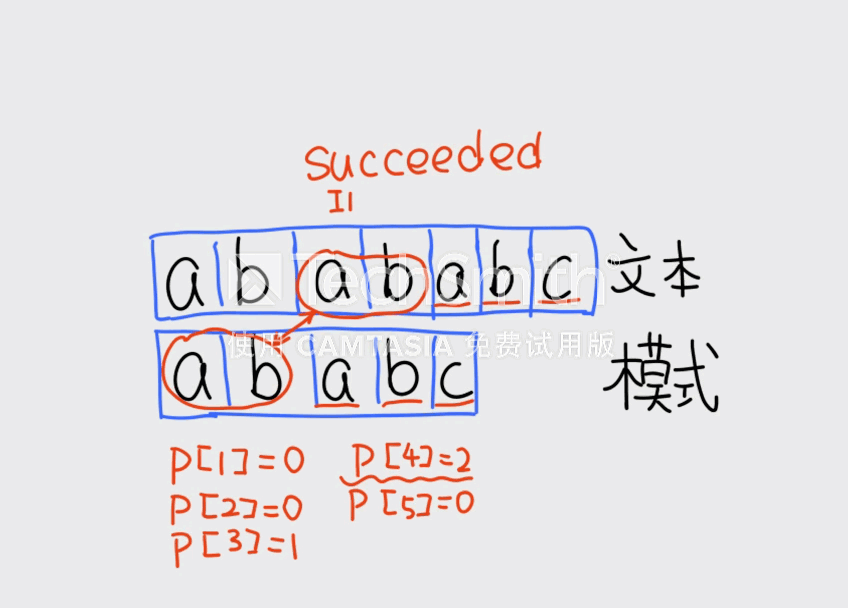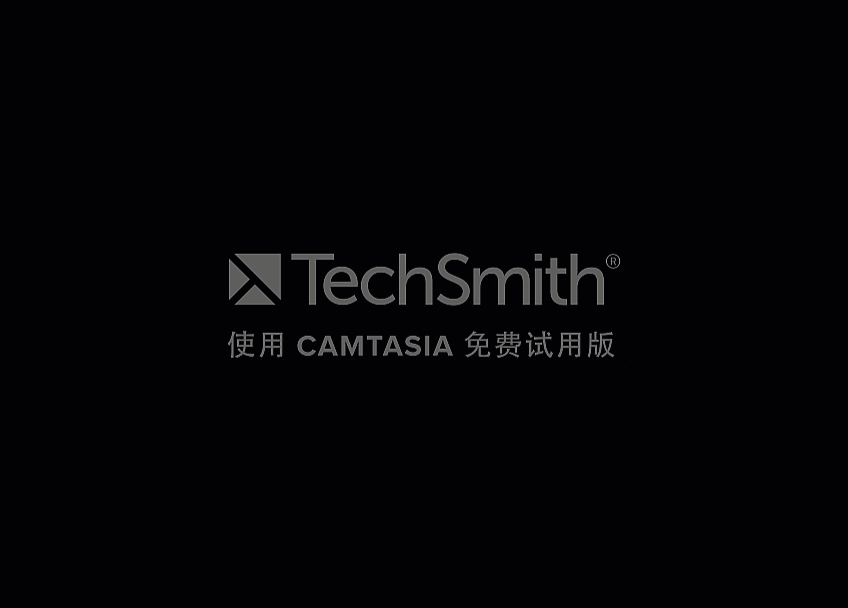
所以我们引入一个 数组:
表示 的前缀 中,最长的 的长度。
求法如下:(思想是「用自己匹配自己」)
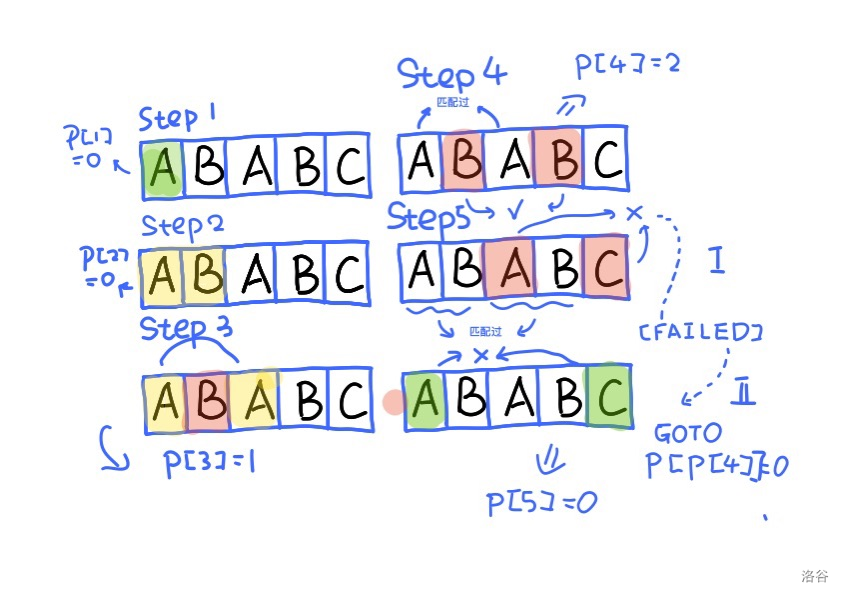
For(i,2,len_b) // p[1] 一定等于 0,故不用求
{
while(j && b[j+1] != b[i]) j=b[j]; // 失配,往回跳
if(b[j+1]==b[i])
++j;
p[i]=j;
}
 有了 数组,我们就可以快捷地利用以求过的信息,快速完成计算啦!
有了 数组,我们就可以快捷地利用以求过的信息,快速完成计算啦!
假设在匹配 和 时失配,我们只要将 之后继续进行计算即可!
For(i,1,len_a)
{
while(j && b[j+1] != a[i]) j=b[j];
if(b[j+1]==a[i]) ++j;
if(j==len_b)
{
cout<<i-j+1<<endl; // 匹配成功
j=b[j];
}
}