#平衡树pre-BST
#Perface
二叉查找树(Binary Search Tree)是一种重要的数据结构,虽然他的用处少之又少,但它是学习平衡树之前必不可少的一环,切勿操之过急,在弄懂二叉查找树之前就开始学习深奥的平衡树。
#Quelity
二叉查找树的性质有以下几条:
- 满足二叉树的所有性质
- ∀u ∈ BST,若 u 左右孩子不空,则 valuelson(u) < valueu < valuerson(u)$
#Achieve
ProbLink
#Node
来看一个 BST 的节点是怎么样的:
struct point{
int v,ch[2],cnt,siz;
};
一个个解释吧:
v : 权值ch: 0是左孩子,1是右孩子。cnt: 值为当前权值的元素有几个。siz: 以当前节点为根子树大小。
#Insert
插入节点。
void Ins(int x,int v)
{
tr[x].siz++;
if(tr[x].v==v){tr[x].cnt++;return ;}
if(v<tr[x].v)
{
if(tr[x].ch[0]) Ins(tr[x].ch[0],v);
else
{
New(v);
tr[x].ch[0]=tot;
}
}
if(v>tr[x].v)
{
if(tr[x].ch[1]) Ins(tr[x].ch[1],v);
else
{
New(v);
tr[x].ch[1]=tot;
}
}
}
#Pre
求比我小的里最大的。
int Pre(int x,int v,int cur)
{
if(tr[x].v>=v)
{
if(!tr[x].ch[0]) return cur;
else return Pre(tr[x].ch[0],v,cur);
}
else
{
if(!tr[x].ch[1]) return tr[x].v;
else return Pre(tr[x].ch[1],v,tr[x].v);
}
}
#Nxt
类比 Pre 。
int Nxt(int x,int v,int cur)
{
if(tr[x].v<=v)
{
if(!tr[x].ch[1]) return cur;
else return Nxt(tr[x].ch[1],v,cur);
}
else
{
if(!tr[x].ch[0]) return tr[x].v;
else return Nxt(tr[x].ch[0],v,tr[x].v);
}
}
#Get rank
按照值找排名。
int Rank(int x,int v)
{
if(!x) return 0;
if(v==tr[x].v) return tr[tr[x].ch[0]].siz;
if(v<tr[x].v) return Rank(tr[x].ch[0],v);
return Rank(tr[x].ch[1],v)+tr[x].cnt+tr[tr[x].ch[0]].siz;
}
#Get val
按照排名找值。
int Val(int x,int rk)
{
if(!x) return INF;
if(tr[tr[x].ch[0]].siz>=rk) return Val(tr[x].ch[0],rk);
if(tr[tr[x].ch[0]].siz+tr[x].cnt>=rk) return tr[x].v;
return Val(tr[x].ch[1],rk-tr[x].cnt-tr[tr[x].ch[0]].siz);
}
#tips
第一次插入时要直接新建节点
#Postscript
这就是 BST 的实现,注意到当插入有序时,它将退化成链表,时间复杂度就寄了。
平衡树的作用就是维护 BST 的深度时刻为 logn ,使得时间复杂度稳定在对数。
不过那,便是以后的事了(鸽qwq)。
#平衡树No.1-FHQ Treap
#Perface
在阅读本文之前,请务必对 BST (二叉查找树)与二叉堆有一定了解。
无旋Treap,又名 fhq Treap,是许多 OIer 的主力平衡树。
它没有旋转操作,并且可以轻易地实现可持久化以及复读机的代码成为了平衡树双子星之一。
%%% fhq %%%
#Treap & fhq Treap
Treap=Tree+Heap
其中,Tree 指的是 BST ,这个等式很好的表达了 Treap 的本质:
利用 BST 的性质实现操作,利用 Heap 的性质维护树平衡。
记住这句话。
要考的
但 fhq Treap ,却不同于传统 Treap 维护时繁琐的旋转,只需要利用好树合并与树分裂即可。
合并与分裂就是它的核心操作。
#Achieve
ProblemLink
rt 为根节点,tot 为节点总数。
#node
struct point{
int ls,rs,v,w,siz;
}trp[mxN];
ls,rs:左右孩子。
v:权值,需保证 BST 的性质。
w:优先值,用于维护树平衡,满足 Heap 的性质,随机生成。
siz:以当前节点为根的子树大小。
#New
int New(int x){
trp[++tot]=(point){0,0,x,rnd(),1};
return tot;
}
rnd用的是 mt19937 。
#pushUp
维护子树大小。
void psu(int p){
trp[p].siz=trp[trp[p].ls].siz+trp[trp[p].rs].siz+1;
}
#split
重头戏来了。
按值分裂是什么????
将当前树分成根节点分别为 x,y 的两棵子树,并且 x 中所有节点的权值小于等于当前值, y 树中的所有节点的权值大于当前值。
上图:
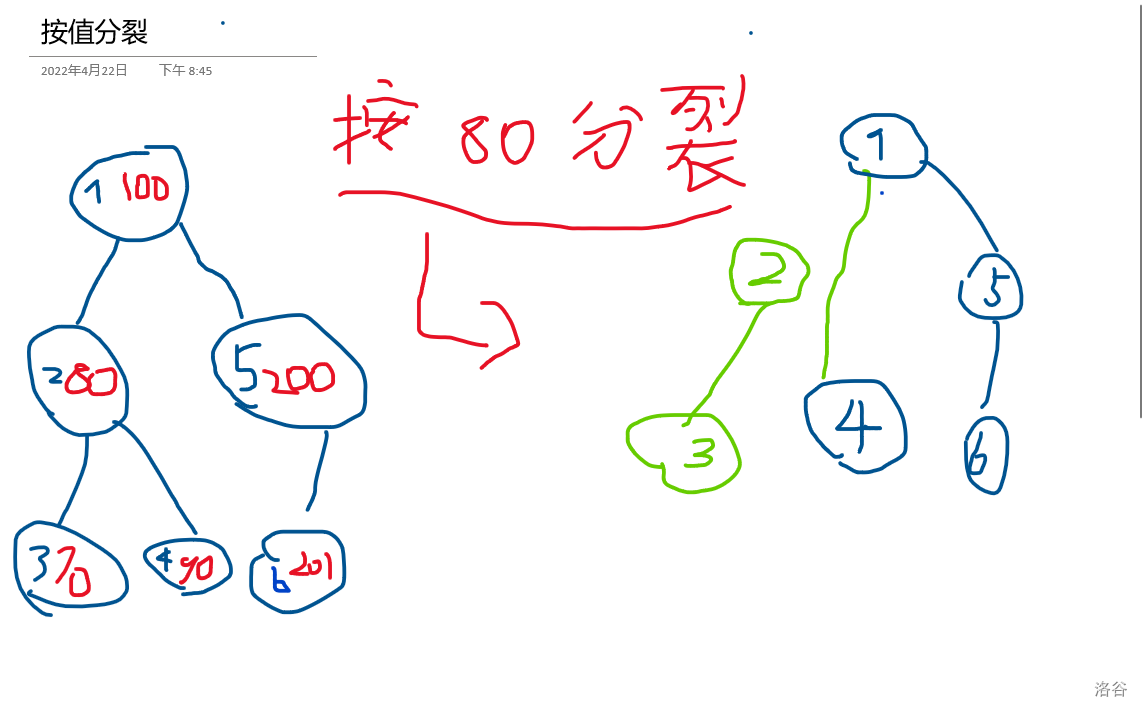
图中蓝笔是编号,红笔是权值,绿笔是改动过的边或点。
void split(int v,int &x,int &y,int p){
if(!p) return x=y=0,void();
if(trp[p].v<=v){
x=p;
split(v,trp[p].rs,y,trp[p].rs);
}
else{
y=p;
split(v,x,trp[p].ls,trp[p].ls);
}
psu(p);
}
#merge
这个比 split 好理解一些。
就是要把以 x,y 作为根节点的两棵子树合并起来,并返回合并后子树根节点编号。
就不放图了,比较简单。
注意要维护 Heap 的性质。
并且 x 树上所有结点的权值小于 y 树上所有节点权值。
int merge(int x,int y)
{
if(!x||!y) return x+y;
if(trp[x].w>trp[y].w)
{
trp[x].rs=merge(trp[x].rs,y);
psu(x);
return x;
}
else
{
trp[y].ls=merge(x,trp[y].ls);
psu(y);
return y;
}
}
后面的操作就很轻松愉快,重点是 Ins & Del。
#Ins
把树拆开,插入值,并回去,没了。
void Ins(int v){
split(v,x,y,rt);
rt=merge(x,merge(New(v),y));
}
#Del
稍微繁琐一点,先按值裂成 x,z。
再把 x 按值减一裂成 x,y。
此时,y 里所有节点值均等于目标值。
合并 y 的左右子树,再把前面分开的树并回去即可。
void Del(int v){
split(v,x,z,rt);
split(v-1,x,y,x);
y=merge(trp[y].ls,trp[y].rs);
rt=merge(merge(x,y),z);
}
后面找排名,找值,找前驱后继都是老生常谈了。
#getRank
int Rank(int v){
split(v-1,x,y,rt);
int rk=trp[x].siz+1;
rt=merge(x,y);
return rk;
}
#getVal
和 BST 没有任何区别,不过此时用循环找优化了常数。
int Val(int rk){
int u=rt;
while(u){
if(trp[trp[u].ls].siz+1==rk) break;
if(trp[trp[u].ls].siz+1>rk) u=trp[u].ls;
else{
rk-=trp[trp[u].ls].siz+1;
u=trp[u].rs;
}
}
return trp[u].v;
}
#Pre
就分裂出比我小的,在比我小的里一直往大了跳。
int Pre(int v){
split(v-1,x,y,rt);
int u=x;
while(trp[u].rs) u=trp[u].rs;
rt=merge(x,y);
return trp[u].v;
}
#Nxt
分裂出大于等于我的,在它们里面往小了跳。
int Nxt(int v){
split(v,x,y,rt);
int u=y;
while(trp[u].ls) u=trp[u].ls;
rt=merge(x,y);
return trp[u].v;
}
#Postscript
是不是又好写又好理解啊?
相信你已经感受到了它的强大,还有更多强大的操作将在后面介绍。
不过,在写动态树时,另一颗双子星—— Splay 是非常必要的,而且一般常数比 fhq Treap 好一些。
所以平衡树的深渊还在前方,祝贺你迈出的第一大步!
